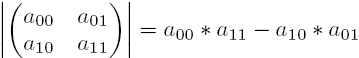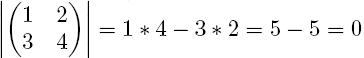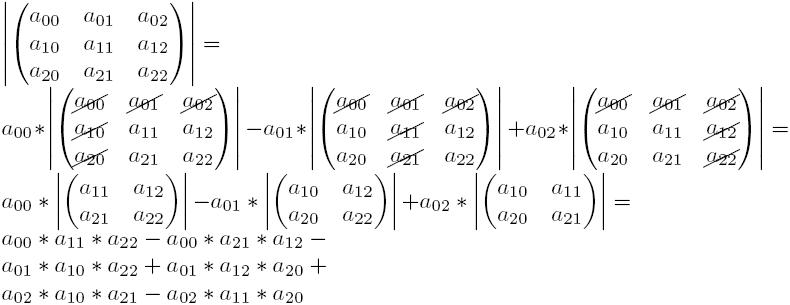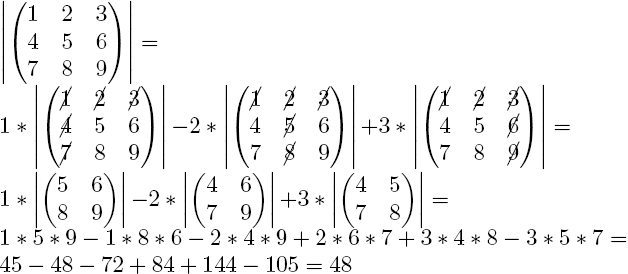You can only calculate the determinant of a squared matrix: where the number
of rows is equal to the number of columns. The determinant for a 2x2 Matrix is simple:

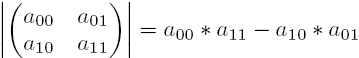
You multiply a00 with a11, and from that you subtract a01, multiplied by a 10.
To give a concrete example:


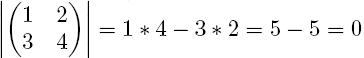
For larger matrices, the process becomes a whole lot more complicated. To illustrate,
here is how you calculate the determinant of a 3x3 matrix:

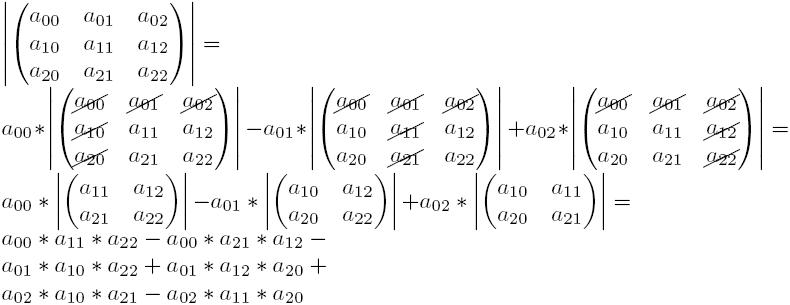
First, you take a row. This can be any row, but for this exercise we keep to the top row.
Then, for every element on that row we calculate the determinant of the elements of
the matrix that don't lie in the same row or column of this element.
You then multiply this determinant with this element, and in case, for element axy, where:
x + y equals an odd number, you multiply it with -1. In our case, you do this with the second,
fourth, etc element of the top row. If you have done this for every element in the row, you
add everything together and the result is the determinant. Here's a concrete example:


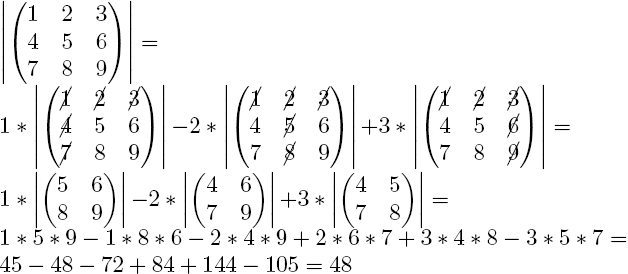
Because of this, if you increase the size of the matrix, this process quickly becomes virtually
impossible. Because of that we limited this exercise to only matrices of size 2, 3 or 4.

In this exercise we broke up the process of calculating the determinant in various stages.
First you need to reduce the matrix into sub-matrices, whose determinants can be calculated easier.
Start from the top-left and fill in the open spaces in the formula by choosing the correct
answer between the three given ones. As soon as only 2x2-matrices are left, you need to
calculate their determinants (as shown above), and multiply and add the rest together until
you get to the right answer.

Go back to the page index